О. Л. Фиговский¹, В. В. Андреев²

¹ INRC Polymate, (Israel) e- mail: figovsky@gmail.cjm

²ФГБОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова»

1. Введение.

Важность математических моделей, описывающих динамику социально-экономической системы, заключается в том, что они позволяют, в частности, учесть в процессе разработки и проведения социально-экономических преобразований наиболее проблемные направления, которые не только представляют собой приоритеты развития, но и являются источниками рисков. Выявление определяющих дальнейшую эволюцию системы тенденций является ключевым элементом при принятии тех или иных управленческих решений. Ранее профессором Фиговским были рассмотрены основные тенденции, сложившихся в динамике социально-экономической системы в России, Израиле и Казахстане [1-3].

Для описания процессов в социально-экономических системах наряду с традиционным статистическим анализом и обработкой данных в последнее время активно разрабатываются методы исследования, основанные на применении подходов, ранее разработанных и используемых в других точных науках, в частности, в физике [4-7]. Также активно развиваются и применяются в исследовании динамики социально- экономических систем модели, относящиеся к классу так называемых моделей «хищник-жертва» [8- 9]. Например, в работе [9] эта модель применена для исследования эволюционной динамики национализма и миграции. Одними из наиболее эффективных приложений модели «хищник-жертва» были исследования рынка труда [10-12]. В работах [13- 15] на основе подобной модели проанализированы циклы занятости и приватизационные циклы и получены важные результаты.

Вообще разнообразные модели популяционной динамики активно применяются для исследования различных процессов социально- экономической динамики [16, 17].

В предыдущих наших работах также предложены и исследованы математические модели динамики социально-экономических систем, построенные на принципах «хищник-жертва» [18- 28]. Эти модели были применены для анализа динамики социально-экономических систем России [18- 22, 27, 28] и США [23- 26] на различных временных этапах. Результаты этих исследований вполне адекватно описывают реальную наблюдаемую ситуацию.

2. Математическая модель.

При построении математической модели динамики социально-экономической системы России будем основываться на подходе, представленном в работе [29]. Этот подход основан на выделении в сложной системе основных подсистем (структурных единиц), определяющих динамику всей системы. Степень детализации при выделении подсистем зависит от цели исследования. С одной стороны, чем большее количество подсистем выделяется, тем более точный конечный результат можно получить. С другой стороны, начиная с некоторого шага, более мелкая детализация подсистем будет приводить лишь к незначительному увеличению точности моделирования (а то и вовсе не давать более точные результаты), приводя при этом к существенному увеличению трудоёмкости расчётов. Выделение основных элементов и движущих сил, определяющих динамику социально-экономической системы, происходит на основе системного подхода и всестороннего анализа системы в целом.

Одна из математических моделей [27-30], ранее использованная авторами для анализа тенденций и трендов в динамике социально- экономической системы России, имеет вид:

                                                                                   (1)

.

В уравнениях (1) коэффициенты α_i, β_i, γ_i, δ_i, и φ_i в общем случае могут зависеть от времени t. Здесь в ходе дальнейших исследования предполагаем их постоянными на исследуемом временном интервале [t₀, t_f].

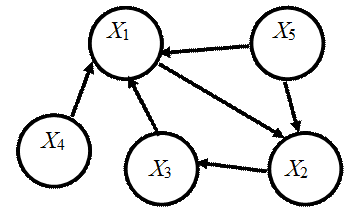
Элементы (подсистемы) этой модели взаимодействуют друг с другом в соответствии со схемой, представленной на рис.1.

Рис. 1. Структурная схема взаимодействия элементов социально- экономической системы.

Здесь стрелка исходит от хищника и заканчивается на жертве. В этой модели в качестве основных элементов, определяющих динамику социально-экономической системы в целом, выбраны: X₁, обозначающий доходы консолидированного бюджета x₁; X₂ – валовой внутренний продукт (ВВП) x₂; элемент X₃ – расходы на финансирование науки x₃; элемент X₄ – доходы населения x₄; элемент X₅ – утечку капиталов x₅. Выбор такого набора взаимодействующих между собой элементов X₁,…, X₅ обоснован тем, что они характеризуют и определяют как темпы социально-экономического развития государства в целом, так и уровень благосостояния населения.

Также необходимо отметить, что в социально-экономической системе, как и в живой природе, часто взаимодействие элементов системы между собой можно трактовать в терминах взаимодействия хищников и жертв. Здесь также происходит поглощение более сильными структурными элементами системы (или подсистемами) более слабых. Более сильные субъекты, почувствовав неустойчивость социально-экономической системы в целом, не вкладывают капитал в развитие экономики, а начинают вывозить его за границу всё в более широких масштабах. Таким образом, «хищник» уничтожает материальные и трудовые богатства государства, которые выступают в данном случае в роли «жертвы». Когда самоцелью социально-экономической политики государства становится, например, рост ВВП без учёта остальных показателей состояния системы в целом и их сбалансированности между собой, то здесь ВВП можно рассматривать в качестве «хищника», поедающего и уничтожающего устойчивость всей системы.

При исследовании динамики сложной системы с помощью систем дифференциальных уравнений вида (1) возникает проблема идентификации неизвестных параметров α_i, β_i, γ_i, δ_i, и φ_i. Для решения задачи идентификации в работах [18-30] использовались данные государственной статистики. Перечисленные неизвестные коэффициенты определяются так, чтобы на заданном временном интервале [t₀, t_f] расхождение между данными государственной статистики и соответствующими им решениями системы дифференциальных уравнений (1), было минимальным. Одним из эффективных методов решения такой задачи идентификации является алгоритм Левенберга- Марквардта в модификации Флетчера [31-34].

3. Применение математической модели (1) для исследования динамики социально-экономической системы России

Обобщая результаты работ [27-30] можно сказать, что модель вида (1) адекватно описывает динамику социально- экономической системы России. Например, из проведённого в работе [27] исследования следует, что модель (1) позволила правильно описать социально- экономическую ситуацию во второй половине 1990-х годов и случившийся в 1998 году дефолт. Кроме того, из анализа, проведённого в работах [27, 28], следует, что кризисные явления после 2000 года особенно нарастали в 2004-2005 и 2011-2012 годах. Эти даты коррелируют с годами президентских выборов в России (2004, 2008, 2012 годы). Относительно 2008 года можно сказать, что выборы тогда проходили на фоне мирового финансового кризиса и локальный кризис в России в 2008-2009 годах наложился на мировой кризис. Из результатов работы [28] также следует, что при сохранении тенденций, сложившихся в социально-экономической системе России к концу 2011 года, очередными особенно тяжёлыми годами будут 2016-2017 годы. Здесь необходимо отметить, что в работе [28] идентификация параметров модели (1) выполнялась по статистическим данным [35, 36] с 2000 по 2011 год включительно.

Проанализируем динамику социально-экономической системы России на основе модели (1) с учётом статистических данных для элементов X₁,…, X₅ с 2005 по 2012 годы. Почему в качестве точки отчёта берётся 2005 год, было подробно исследовано в работе [28]. Таким образом, для идентификации неизвестных параметров модели (1) используем данные статистики с 2005 по 2012 год включительно. Определяем оптимальный вектор параметров α_i, β_i, γ_i, δ_i, и φ_i модели (1), для которого решения x_i(t), i=1,2,…5 наиболее точно количественно и качественно описывают соответствующие статистические данные за рассматриваемый период времени. Идентификация параметров системы дифференциальных уравнений (1) на временном интервале с 2005 по 2012 годы дала следующие оптимальные значения:

α₁=0,0098, α₂=0,00158, α₃= -5,8111∙10^-4, α₄=0,0021, α₅=0,09122,

β₁=-8,0666∙10^-4, β₂=-3,7113∙10^-4, β₃=3,8624∙10^-4, β₄= -0,01947,

γ₁=0,002517, γ₂=9,4216∙10^-4, γ₃= -0,07443,                                                                                (2)

δ₁=-3,8554∙10^-4, δ₂= -0,0935,

φ₁=0,00857_, φ₂= -0,00232_, φ₃=0,259.

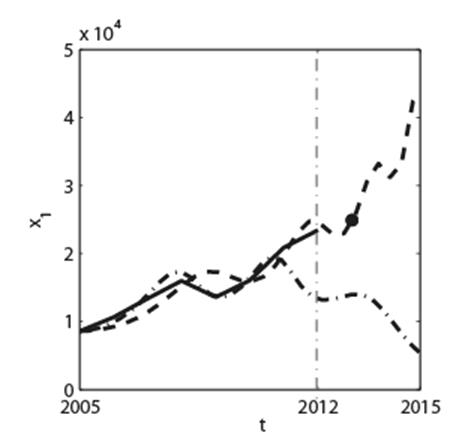
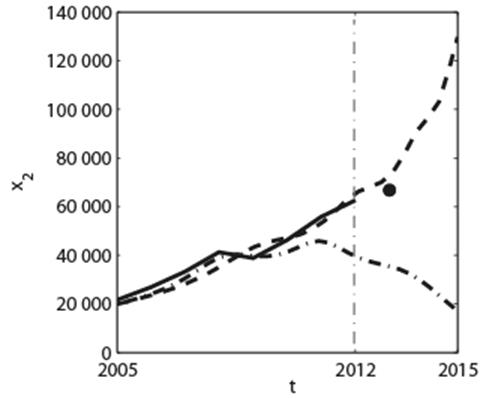
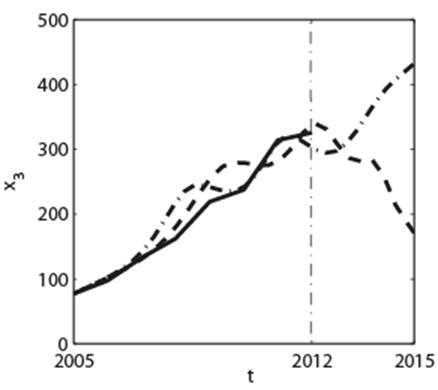
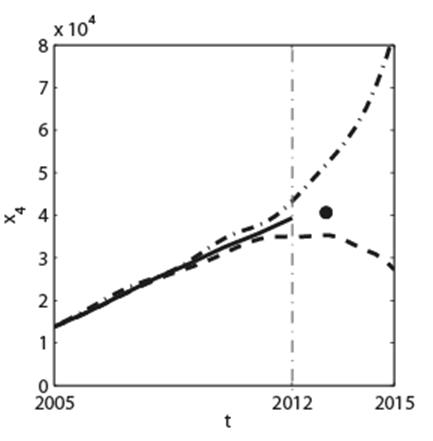
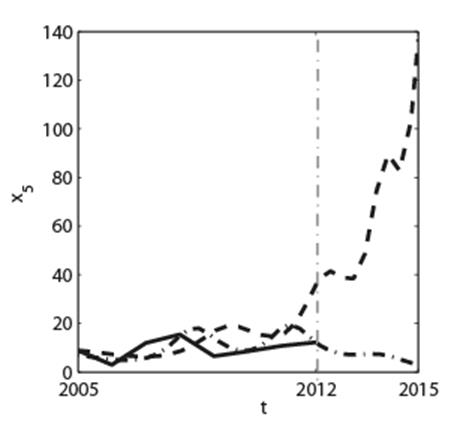
Зависимости x_i(t), i=1,2,…5, полученные численным решением системы дифференциальных уравнений (1) с коэффициентами (2), представлены на рис.2 (штриховые кривые). Сплошные кривые на рис.2 соответствуют статистическим данным. Начальные условия x_i(t₀=2005 год), i=1,2,…5 задавались равными соответствующим статистическим данным в 2005 году.

Штрихпунктирные кривые на рис.2 соответствуют решениям x_i(t), i=1,2,…5 системы дифференциальных уравнений (1) в случае, когда для идентификации неизвестных параметров математической модели использовались статистические данные с 2005 по 2011 год включительно. Начальные условия, как и в предыдущем случае, задавались равными соответствующим статистическим данным в 2005 году. В этом случае оптимальные значения коэффициентов модели (1) следующие:

α₁=0,001, α₂=0,0015, α₃= -5,1099∙10^-4, α₄=0,002, α₅=0,0913,

β₁=-8,2943∙10^-4, β₂=-4,6010∙10^-4, β₃=4,0486∙10^-4, β₄= -0,0193,

γ₁=0,0024, γ₂=9,6204∙10^-4, γ₃= -0,0744,                                                                                       (3)

δ₁=-4,0673∙10^-4, δ₂= -0,0937,

φ₁=0,0091_, φ₂= -0,0027_, φ₃=0,2587.

Штриховые кривые на рис.2, продолженные за границу 2012 года, отображают в терминах элементов X₁,…, X₅ динамику социально-экономической системы России после 2012 года в случае, если сохранятся те же самые тенденции, которые сложились в системе к концу 2012 года. Аналогично, штрихпунктирные кривые на рис.2 показывают динамику социально-экономической системы в случае, если сохранились бы без изменений тенденции, сложившиеся в системе к концу 2011 года.

Рис. 2. Результаты моделирования: сплошные кривые соответствуют данным статистики с 2005 по 2012 годы; штриховые кривые являются решениями модели (1), полученными при идентификации параметров по статистическим данным с 2005 по 2012 годы; штрихпунктирные кривые – решения модели (1), полученные при идентификации параметров по статистическим данным с 2005 по 2011 годы. По оси абсцисс время t отложено в годах. По осям ординат представлены следующие функции: x₁, обозначающая доходы консолидированного бюджета, в млрд. руб.; x₂, описывающая динамику ВВП, в млрд. руб.; x₃, представляющая расходы на финансирование науки, в млрд. руб.; x₄, описывающая динамику доходов населения страны, в млрд. руб.; x₅, описывающая динамику утечки капитала из страны, в млрд. долл. Жирные точки на зависимостях x₁(t), x₂(t) и x₃(t) обозначают статистические данные в конце 2013 года.

Из сравнения наборов параметров (2) и (3) модели (1) видно, что наиболее существенно (почти в 10 раз) изменился лишь α₁, а остальные параметры изменились незначительно. Однако в результате решения модели (1) в долгосрочной перспективе качественно поменяли свой характер. Параметр α₁ входит в первое уравнение модели (1) как коэффициент перед произведением α₁x₁x₂. Функция x₁(t) описывает динамику доходов консолидированного бюджета, а x₂(t) – динамику ВВП.

Из этого можно заключить, что в 2012 году после президентских выборов произошла корректировка проводимого в стране социально-экономического курса в плане коррекции динамики доходов консолидированного бюджета и ВВП. Так, в случае штрихпунктирных кривых на рис.2 падение после 2011 года доходов консолидированного бюджета (x₁) и ВВП (x₂) при одновременном росте расходов на финансирование науки (x₃) и доходов населения (x₄) означает возникновение высокого уровня инфляции и, соответственно, печатание ничем не обеспеченной денежной массы.

Пересмотр политики в социально-экономической сфере в 2012 году, вероятно, состоял в том, чтобы обеспечить в ближайшие годы непрерывный рост доходов консолидированного бюджета и ВВП (штриховые кривые на рис.2). Однако при этом появляется тенденция падения расходов на финансирование науки и доходов населения (см. штриховые кривые x₃(t) и x₄(t) соответственно на рис.2).

В то же время после 2012 года при сложившейся тенденции вывоз капитала из страны увеличивается (штриховая кривая x₅(t) на рис.2). Это означает, что в стране реализовывается курс на повышение доходов консолидированного бюджета и ВВП без вложения достаточных финансовых средств на развитие социально-экономической сферы. Такие тенденции в динамике социально-экономической системы России, которые сложились к концу 2012 года, при их сохранении в ближайшие годы приведут к крайне нестабильной ситуации в стране.

В то же время в работе [28] было отмечено, что в случае развития социально-экономической системы России в соответствии с тенденциями, сложившимися к концу 2011 года, она срывается в так называемый режим с обострением к 2017 году. Под режимом с обострением понимается такое поведение одной или нескольких функций x_i(t), когда она начинает неограниченно расти за малый интервал времени Δt [37, 38]. Очевидно, никакая реальная система не обладает ресурсами, чтобы устойчиво функционировать в режиме с обострением. Анализ штриховых кривых на рис.2 показывает, что тенденция срыва системы в режим с обострением не изменилась. Возможно при тенденциях, наметившихся в 2012 году, срыв социально-экономической системы России в режим с обострением может произойти немного раньше 2017 года. Об этом свидетельствует быстрый рост функций x₂(t) и x₅(t) (см. штриховые кривые на рис.2).

На зависимостях x₁(t), x₂(t) и x₄(t) (см. рис.2) жирной точкой обозначены статистические данные в конце 2013 года. Они достаточно хорошо коррелируют с тенденцией поведения штриховых кривых на рис.2. Расходы на финансирование науки в 2013 году составили около 400 млрд. рублей [35, 36]. Отток капитала из России по итогам 2013 года превысил 60 млрд. долл. Эти данные также хорошо коррелируют с тенденцией поведения штриховых кривых x₃(t) и x₅(t) соответственно на рис.2.

4. Заключение.

Таким образом, можно сделать вывод, что в России отсутствуют как краткосрочные, так и долгосрочные планы социально-экономического развития. Социально-экономическая политика государства проводится от очередных президентских выборов до следующих.

Также можно утверждать, что обостряющийся в настоящее время в социально-экономической сфере России кризис не является напрямую следствием введённых в 2014 и в 2015 годах санкций. Этот кризис является результатом не принятых своевременно мер по стабилизации и развитию социально-экономической системы органами власти России.

Исследованная модель (1) позволяет определить тенденции, складывающиеся в динамике социально-экономической системы. На основе модели (1) также можно определить режимы длительного функционирования системы в устойчивых бескризисных состояниях. Безусловно, моделирование и анализ развития тенденций в социально-экономической сфере крайне важны для своевременного принятия оптимальных управленческих решений. Это особенно важно в условиях проведения социально-экономических преобразований в период кризисного характера происходящих процессов.

Литература.

1. Фиговский О. Эергетический уклад человечества меняется. Институт эволюционной экономики, 2015 - http://iee.org.ua/ru/publication/272/

2. Фиговский О. Желающий ехать – быстрей езжай. Желающий действовать - действуй. 31.Институт Интеграционных Исследований. 27.07.2015. http://www.figovsky.iri-as.org/stat/02_57_wishtoride.PDF

3. Фиговский О. Не импортозамещение, я создание принципиально нового. Наука и жизнь Израиля. 31.012015

4. Mantegna R.N., Stanley H.E. An introduction to econophysics: correlations and complexity in finance. Cambridge University Press, 2000. 148 p.

5. Econophysics of Systemic Risk and Network Dynamics (New Economic Windows) / By Edition Frédéric Abergel, Bikas K. Chakrabarti, Anirban Chakraborti, Asim Ghosh. Springer, 2013. 306 p.

6. Giovani L. Vasconcelos. A guided walk down wall street: an introduction to econophysics // Brazilian Journal of Physics, 2004, v.34, №03B. P. 1039-1065.

7. Castellano C., Fortunato S., Loreto V. Statistical physics of social dynamics //Reviews of Modern Physics, 2009, v. 81, №2, p. 591-646.

8. Shengmao Fu, Lina Zhang, Ping Hu. Global Behavior of Solutions in a Lotka- Volterra Predator- Prey Model with Prey-Stage Structure // Nonlinear Analysis: Real World Applications, 2013, v. 14, p. 2027- 2045.

9. Kazuhito Yamasaki, Takahiro Yajima. Lotka- Volterra System and KCC Theory: Differential Geometric Structure of Competitions and Predations // Nonlinear Analysis: Real World Applications, 2013, v. 14, p. 1845- 1853.

10. Qiu Xiao-xiao, Xiao Hai-bin. Qualitative Analysis of Holling Type II Predator- Prey Systems with Prey Refuges and Predator Restricts // Nonlinear Analysis: Real World Applications, 2013, v. 14, p. 1896- 1906.

11. Jiafu Wang, Xiangnan Zhou, Lihong Huang. Hopf Bifurcation and Multiple Periodic Solutions in Lotka- Volterra Systems with Symmetries // Nonlinear Analysis: Real World Applications, 2013, v. 14, p. 1817- 1828.

12. André Barreira da Silva Rocha. Evolutionary Dynamics of Nationalism and Migration // Physica A, 2013, v. 302, p. 3183- 3197.

13. Коровкин А.Г., Наумов А.В. Социально-экономические проблемы формирования рациональной занятости // Экономика и математические методы, 1990, №5 с.861-870.

14. Коровкин А.Г., Лапина Т.Д., Полежаев А.В. Согласование спроса на рабочую силу и ее предложения: федеральный и региональный аспекты // Проблемы прогнозирования, 2000, №4, с.73-88.

15. Коровкин А.Г. Динамика занятости и рынка труда: вопросы макроэкономического анализа и прогнозирования.- М.: МАКС Пресс, 2001, 320 с.

16. Балацкий Е.В., Екимова Н.А. Типология приватизационных циклов // Общество и экономика, 2007, №9-10, с. 66 - 85.

17. Балацкий Е.В., Екимова Н.А. Влияние конкуренции на длительность и амплитуду приватизационного цикла // Общество и экономика, 2009, №1, с. 21-39.

18. Балацкий Е.В., Екимова Н.А. Цикл занятости и приватизационный цикл в динамических моделях равновесия // Общество и экономика, 2010, №12, с.33-51.

19. Medvinsky A.B., Rusakov A.V. Chaos and Order in Stateless Societies: Intercommunity Exchange as a Factor Impacting the population Dynamical Patterns // Chaos, Solitons and Fractals, 2011, v. 44, p. 390- 400.

20. Медвинский А.Б., Нефёдов С.А., Русаков А.В. Предсказуемость социодинамики (на примере математической модели крестьянской общины) // Нелинейный мир, 2012, №10, с. 189-197.

21. Андреев В.В., Карпова О.В. Математическое моделирование социально- экономических процессов в России конца XX и начала XXI веков // Нелинейный мир, 2007, т.5, №12. с. 773- 777.

22. Карпова О.В., Андреев В.В. Моделирование динамики одной социально- экономической системы на основе модели типа «хищник- жертва» // Математика. Компьютер. Образование: Сб. научных трудов. Том 1 / Под ред. Г.Ю.Ризниченко.– М.-Ижевск: НИЦ «Регулярная и хаотическая динамика». 2007. С. 194-202.

23. Карпова О.В., Андреев В.В. Исследование социально-экономической динамики России на основе модели типа «хищник–жертва» // Математика. Компьютер. Образование: Cб. трудов XV международной конференции. Том 1/ Под общей редакцией Г.Ю. Ризниченко. – М.-Ижевск: Научно-издательский центр «Регулярная и хаотическая динамика». 2008. С. 231-236.

24. Андреев В.В., Карпова О.В. Попытка построения математической модели социально- экономической системы: исследование на примере Чувашской Республики // Вестник Чувашского университета. Гуманитарные науки, 2008, №1, с.385- 390.

25. Андреев В.В., Ярмулина О.О. Математическое моделирование динамики социально-экономической системы (на примере России) // Нелинейный мир, 2009, т.7, №6, с.464- 474.

26. Андреев В.В., Семёнов М.И. Программное приложение для решения задач оптимальной параметрической идентификации динамических моделей: применение для прогнозирования динамики социально-экономической системы США// Прикладная информатика, 2010, №2(26), с.46-57.

27. Андреев В.В., Семёнов М.И. Математическое моделирование и исследование динамики социально- экономической системы (на примере США) // Нелинейный мир, 2010, т.8, №3, с.189- 195.

28. Андреев В.В., Семёнов М.И. Моделирование динамики социально- экономической системы на примере США // Математика. Компьютер. Образование: Сб. научн. трудов. Том 2 / Под ред. Г.Ю. Ризниченко. – М.- Ижевск: НИЦ «Регулярная и хаотическая динамика». 2010. С.236- 246.

29. Андреев В.В., Семёнов М.И. Математическое моделирование динамики социально- экономической системы США // Нелинейный мир, 2012, т.10, №5, с.322-330.

30. Андреев В.В., Васильева Е.А. Математическое моделирование и исследование динамики социально- экономической системы России // Известия РАЕН. Дифференциальные уравнения, 2009, № 14, с.25-38.

31. Андреев В.В., Семёнов М.И. Математическое моделирование динамики социально- экономической системы России: определение наилучшего пути развития // Нелинейный мир, 2013, т.11, №1, с.58- 72.

32. Andreev V.V. On the validity of use of physical equations and principles in the socio-economic field and on the predictability of socio-economic system dynamics // Nonlinear Analysis: Modelling and Control, 2015, v. 20, №1, p.82-98.

33. Andreev V.V. Will there be a revolution in Russia in 2017? // Journal of Policy Modeling, 2015, http://dx.doi.org/10.1016/j.jpolmod.2015.06.001

34. Gill P.E., Murray W., Wright M.H. Practical Optimization. New York: Academic Press, 1981. 418 p.

35. Levenberg K. A Method for the Solution of Certain Problems in Least Squares // Quart. Appl. Math, 1944, v.2, p.164-168.

36. Marquardt D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters // SIAM J. Appl. Math., 1963, v.11. p. 431- 441.

37. Fletcher R. A Modified Marquardt Subroutine for Nonlinear Least Squares // Rpt. AERE-R 6799, Harwell, 1971.

38. htt://www.gks.ru - Федеральная служба государственной статистики. Российский статистический ежегодник.

39. http://www.cbr.ru - Банк России. Статистика. Платежный баланс и внешний долг Российской Федерации.

40. Князева Е.Н., Курдюмов С.П. Основания синергетики. Режимы с обострением, самоорганизация, темпомиры. СПб.: Алетейя. 2002. 416 с.

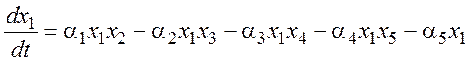
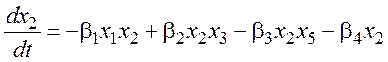
41. Белавин В.А., Курдюмов С.П. Режимы с обострением в демографической системе. Сценарий усиления нелинейности// Журнал вычислительной математики и математической физики. 2000. Т.40. №2. С. 238- 25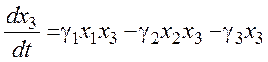1.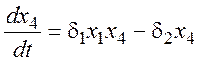
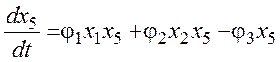