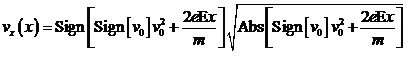Преамбула.

Просматривая научные новости и форумы, я постоянно сталкиваюсь с тем, что соображения, изложенные в моих предыдущих статьях, скорее доходят до клерков, старающихся спекулировать на идеях, чем до широкой научной общественности. Это плохо, но при том плачевном состоянии, в каком находится наука в России, это естественно. Когда реальную помощь на исследование, на идею, если ты не кум, сват, брат какого-либо чинуши, можно получить лишь из-за бугра, а «кумовья» лишь помогают отмывать деньги и пристраивать подрастающих «кумов», российским учёным «надо» быть послушными к зарубежному мнению. Когда в российские научные журналы часто пишут для галочки (для отчётности, для ПРНД для символической надбавки к символической зарплате), т.к. эти журналы многие российские исследователи сами и не читают. Если же в них пишут, то в надежде лишь на то, что кого-то это заинтересует опять же за бугром - даже в ЖЭТФе размещают иногда статьи сразу на английском.

Но, сконцентрировавшись в прошедшем году на научно-популярных статьях (даже в ущерб чисто научным), я хотел, всё-таки, дать фору останкам российских учёных на будущее. Они, по большому счёту уже давно содержат научную бюрократию, а не она их (что входит в её прямые обязанности, но она СОБОЙ жертвовать ради НАУКИ не «обучена») и, тем самым, останки начинают сметь проявлять «варварскую» самостоятельность – крепостное право научных бюрократов в России заканчивается а субординация, позаимствованная ими из армии, в которой они никогда не бывали, никогда не была приоритетом истинной науки. Как бы ни хвастались ковальчуки и прочие акдемики МегаДеньгами, перельманы не продают ИСТИНУ.

Также, не публикуя свои последние научно-технические результаты уже два года, я пытался дать фору российской оборонке. И тоже, в первую очередь, не чинушам оборонки, а тем останкам рядовых разработчиков, которых находил, пробивая через чинуш новое направление в технике.

Но, естественно, так продолжать до конца жизни я не считаю целесообразным – страдает и наука, и российская оборонка.

Тем более, что по слухам, в мои статьи даже на нашем русскоязычном сайте всё равно уже заглядывают и из Англии, и из Кореи, и из Японии, и из Китая, и из Бразилии, и из Норвегии, и из Австралии, и, скорее всего, и из Штатов, несмотря на то, что госдеп давно, как мне говорили, внёс меня в «чёрный список» (задолго до списка Магницкого).

Тем более, что в русле уже опубликованных мною ранее идей за рубежом уже вовсю ведут работы, и можно оказаться в хвосте. Тем более, что в русле этих идей, обоснованных в открытой печати преимущественно на качественном уровне, уже ведут работы и на Cree, и на Dexter, и на Samsung, и, думаю, на многих других предприятиях за рубежом, где деньги тратят на дело, а не на липовые отчёты. А у нас пока, даже в оборонке, в лучшем случае какой-нибудь чинуша эти идеи использует для нового «красивого» отчёта, снисходительно сказав другому чинуше: «Да ребята тут какую-то херню предлагают – говорят о хорошо известных вещах, но говорят, что их надо понимать иначе, муть какая-то» (как я узнал через полгода после доклада).

Поэтому пока в России основной ориентир и в политике, и в экономике, и в науке, и в оборонке - на «цивилизованное» забугорье. Чтобы сдвинуть науку в самой России с мёртвой точки, надо прилагать усилия не только в России, а и там, где люди имеют возможность работать под заявленные цели.

Так что приступаю, после этой статьи, к воздействию теми рычагами, на которые и ориентируются наши чинуши и в науке, и в государстве – по-английски. Возможно не только российскую науку, но и российскую оборонку придётся крепить из-за бугра, через ДАРПА. Обозначенный мной ей срок, 1 января, чинуши не выдержали, попросили ещё немного подождать. Ещё немного подожду. Хотя вижу, что проблема та же – не хотят головой рисковать за один нецелевым образом растраченный рубль, зная меня, понимают, что так и будет, и пытаются подкупить ребят, которым я доверил организационные вопросы. Но у нас под заявленные цели и российские деньги не поступают, и выклянченные из-за бугра «инвестиции» не поступают, если их контролируют только чинуши. И это сейчас в России главная проблема, а рыночная экономика – лишь удобное для её сокрытия прикрытие. И исходит эта проблема от «окультуренных» варваров, как в президиуме РАН, так и в других бюрократических структурах. И поэтому, видимо, придётся отвлечься от науки.

Вначале я на последок хотел написать сухую академическую статью (предполагаемую статью «НАНО и ЖИЗНЬ» сейчас, наверное, не потяну и включил в эту лишь отдельные штрихи). Но, потом, подумал, что «детективная» история с пропущенным наноизмерением более живо покажет, что мы в науке пропустили (упустили, растратили) и ещё один важный инвариант – поиск ИСТИНЫ, без которого наука не НАУКА, и не абстрактная, а реальная «тепловая смерть» грозит человечеству, если оно будет оставаться НЕРАЗУМНЫМ объединением РАЗУМНЫХ индивидуумов.

Часть 1. Катастрофы и бесконечности производных.

Многие катастрофические, в обыденном смысле, явления, при внимательном рассмотрении, выглядят не столь катастрофично. Так водопад, «катастрофическое» падение воды с обрыва, описывается медленной, всего лишь квадратичной зависимостью. Не намного круче, резче зависимость торможения пули или автомобиля при столкновением с препятствием. В физике, реальные «катастрофические» (мгновенные, ступенчатые) процессы, типа взрыва, описываются очень быстрыми, экспоненциальными зависимостями. А когда используют дельта–функции, то их нормируют так, что в измеримых зависимостях остаётся «скромный» скачок.

Но если аналитически продолжить частную закономерность, то можно в определенной точке (за пределами применимости этой частной зависимости) получить производную честно (без всякой нормировки) «равную» бесконечности, что и воспринимается как один из видов «катастроф». Например, Бозе-конденсация, переход в сверхпроводящее состояние первоначально, полагали, происходит при строго определённой температуре и теоретики долго с негодованием отвергали результаты экспериментов по предпереходу и послепереходу из состояния с нормальной электропроводностью в сверхпроводящее состояние (это была катастрофа их первоначальных моделей).

Другой пример, граница обычного фазового перехода. Во многих учебниках она до сих пор изображается линией, тогда как после анализа фазовых переходов по нелифшицевской звезде (симметрийная характеристика перехода) стало ясно, что между строго соразмерными состояниями существует не как исключение, а как правило, несоразмерная фаза. Причем, в таких кристаллах как высший силицид марганца (ВСМ), при определённых составах, температурный интервал между строго соразмерными фазами может превышать 500 ^оС. В этом интервале температур термодинамически равновесными являются структуры с концентрационными солитонами, аналогично тому, как в сегнетоэлектриках возникают границы доменов. Даже в хорошо изученном кварце, в конце концов, установили, что граница фазового перехода размыта более чем на градус. В любимой же теоретиками модели прямоугольной потенциальной ямы мы имеем бесконечный градиент потенциала на краю ямы. И если это предположение не соблюдается даже на границе макрообъекта (эффект Шоттки), то упорство, с каким эту упрощённую модель часто использовали на микромасштабе, и продолжают использовать на наномасштабе, представляет собой попытку подогнать Природу под уже решённую математическую задачу.

«Катастрофа» в понимании структуры графита и нитрида бора, которую я сам когда то «спровоцировал», тоже связана с нулями и бесконечностями, приписанными Природе современной физикой: нулевая жесткость связи между слоями и бесконечное отношение жёсткости внутрислоевых и межслоевых связей. Так как я привык анализировать закономерности, а не отдельные значения (которые всегда можно подогнать под рабочую модель), то, столкнувшись с «аномалиями» свойств несоразмерных кристаллов, я решил экспериментально проверить используемые модели на асимптотиках, на канонизированных двумерных кристаллах: C и BN. Нарушение двумерности в этих кристаллах считалось малой поправкой (и экспериментальной погрешностью измерений + несовершенством реальных кристаллов). Но, как показали эксперименты, жесткость межслоевых и внутрислоевых связей между атомами у этих «канонизированных» двумерных кристаллов отличается всего лишь в полтора раза, и, как показал анализ, этот вывод прекрасно согласуется со всеми ранее полученными экспериментальными данными (S.V. Ordin, [B.N. Sharupin], J. Semiconductors (FTP), 32(9), 924-932, 1998, Normal Lattice Oscillations and Crystalline Structure of Non-Isotropic Modifications of a Boron Nitride.). Более того, канонизированная модель Вейса зонной структуры графита, построенная на базе «двумерного» предположения, тоже, естественно, не соответствует реальности (Ordin S.V., Rumyantsev V.I., Tupitsina E.V., Osmakov A.S., Avdeev O.V., Fedorov M.I., Features of Band Structure and Seebeck Coefficient Anisotropy of Pyrographites, Proceedings of VI Interstate Seminar: Thermoelectrics and their applications, October, 1998, St.-Petersburg, Publishing House of the Russian Academy of Science, 1999, p. 123-130, p.278-279.).

Так, казалось бы, чисто проверочный эксперимент дал на выходе подтверждение вывода о том, что, грубо говоря, можно сформулировать так: В ПРИРОДЕ МОДЕЛЕЙ НЕ БЫВАЕТ! Модели описывают природу лишь в границах их применимости. Истинные КОРИФЕИ НАУКИ, заложившие основы современной науки, это хорошо осознавали и скромно старались оговорить условия применения их моделей. Дельцы же от науки (в основном они просто развиватели установленных до них принципов) старались, наоборот, прикрыть свою научную импотенцию уЗАКОНиванием их (а чаще, присвоенных ими) научных результатов.

Так, на мой взгляд, обстоит дело и с некоторыми чисто теоретическими фантазиями. Пусть там формулы и посложнее - теоретические спекуляции, в основном идут на формулах, сложноватых для физиков, основную часть времени занимающихся экспериментами, и примитивных даже для рядовых математиков. Тоже «открытие» «Большого взрыва» в модели пространства-времени, просто указывает на то, что используемая модель не в состоянии описать процессы на затронутых (анализируемых) больших и малых масштабах.

Аналогично, и с «частицей Бога» в теории элементарных частиц, которая, используя очень ограниченный набор экспериментальных методик, преимущественно треки, «с головой» ушла в теоретизирование МЕТОДИК обработки этих результатов. И аналогично тому, как примитивная эмпирическая технология + технология Фотошопа + Википедия + элементарное невежество помноженное на отсутствие сдерживающего Морального Права дали на выходе нобелевский «графеновый вирус» http://rusnor.org/pubs/articles/7782.htm, теоретизирование вокруг примитивных треков «затмило» реальность и родило «теоретический вирус» в виде «частицы Бога» (см. «Непричёсанная физика и частица Бога» http://rusnor.org/pubs/articles/8058.htm ). «Теоретический вирус», циклически ударил по самой теории. Одна двусмысленность названия – осколочек (обломочек) от Бога, говорит об идейном скудоумии авторов, думающих лишь о решении уравнения, а не о Природе. Так на выходе мы имеем мультипликацию (и в прямом смысле – размножение, бесконечный ряд, и в переносном мультики) инвариантов – якобы ЗАКОНОВ СОХРАНЕНИЯ «шарма», «вкуса», «цвета» и тому подобного, и мультипликацию элементарных частиц (сейчас уже «спецы» на БАКе поговаривают о двух бозонах Хиггса).

Когда люди смогут в эти масштабы «копнуть» получше, то найдут неучтённые в частной модели факторы (силы), и найдут закономерности, соответствующие многочисленным реальным процессам на данных масштабах, и смогут связно рассказать, что же они РАСЧИТЫВАЮТ на данном масштабе. А пока что они РАСЧИТЫВАЮТ просто формулы и не могут объяснить, что за этими формулами стоит. А пока что «Большой Взрыв» и «Частица Бога» - это из разряда «катастроф» определённых моделей, а не ПРИРОДЫ. И роль физики я вижу в описании, а не в придумывании Природы. До этого уровня, как в сериале «Грань», мы пока не доросли.

Вторжение в нашу жизнь компьютеров позволило «воочию» нам пронаблюдать некоторые негативные, катастрофические процессы, которые протекали в самой науке последнее столетие. Фрагментированное программирование даёт на выходе программы, содержащие многочисленные функциональные ошибки, которые, толковые программисты стараются исправлять, а озабоченные лишь деньгами – стараются заблокировать – сделать «пробку» в программе (в первую очередь – пользователю, чтобы он не видел ошибок, но иногда и работе самой программы). При этом в виду не идейной, а денежной монополии Виндоуса (см. «Компьютерный вирус» http://rusnor.org/pubs/articles/7892.htm), большинство программ делается под него. Но очень часто эти программы элементарно паразитируют на функциях, заложенных в Операционную Систему, т.е. опять же именно в Виндоус (почему он и зависает, столкнувшись с «пробкой»). Но сам Виндоус является эклектикой слабосогласованных фрагментов. А когда найденную программную «изюминку» автор пытается внедрить во весь Мир Виндоуса, то доводит свою программу до монстра, с которым и работать неудобно, и который ещё больше портит сам Виндоус.

В такой «интеллектуальной» игре, где нет «Интеллектуальных Законов» (и их открывателей – Ломоносовых, Эйнштейнов, Планков) талантливые эмпирики – хакеры определяют прогресс в программировании. Как технологи от бога создают по наитию новые материалы и устройства, или как классные электронщики (не все ещё в России вымерли) создают по наитию уникальные приборы, так хакеры вынуждают программистов искать прорехи в своих программах. Один из таких электронщиков говорил мне, что если собрать сложную схему строго по формулам, то она работать не будет, а когда её по некоторым эмпирическим (опытным) закономерностям подправишь – заработает, так и хакеры по эмпирическим наблюдениям, владея кодировками, создают то, что работать по компьютерной «науке» не должно (но работает). Эти эмпирики сейчас, в основном, и определяют прогресс и в физике, а не теоретики, не имеющие связного общего современного описания Природы.

Но это не есть прогресс в осмыслении Природы. Это перебор уже известных кубиков, в который по наитию иногда вставляют недостающее нечто, что кажется безрассудным (теоретически не обоснованном). Теоретические же попытки с помощью уже известных кубиков описать и то, что лежит за рамками канонизированных моделей – не более чем спекуляция, научная софистика, которая и приводит то к «катастрофе кристаллофизики», то к «инфракрасной», то к «ультрафиолетовой катастрофе», то к «графену». Когда-то Маттиас был рекордсменом в достижении максимальной температуры сверхпроводимости на металлических сплавах, пользуясь лишь эмпирическими закономерностями, а его брошюрка менее 20 страниц противостояла десяткам теоретических томов. Так и сейчас, большинство современных достижений в области НАНО сделано эмпирически, так как пока что нанофизика (тоже уже имеющая десятки томов) базируется на макроскопических представлениях. И основной тормоз в развитии нанофизики связан с не учитываемым параметром – специфической нормальной координатой наномасштаба. Так аномальность теории приводит к «аномальным» явлениям и «открытиям», которых и до НАНО было обнаружено и сделано за сто лет много, но большинство которых уже никого не интересует и в макрофизике.

Часть 2. Размерность явления.

Заранее приношу извинение за «разжёвывание» некоторых аспектов, указывающих на математическую необходимость учета наноинвариантов и нанокоординат, которые до работ Ильи Пригожина не только не учитывались, но и запрещались к рассмотрению, как якобы противоречащие законам сохранения. Но за многочисленными спекулятивными исследованиями «размерных» (dimensional) наноэффектов в нашем 3-х (4-х) мерном Мире (см. «Размерные эффекты и НАНО» http://rusnor.org/pubs/articles/7724.htm) выпал из рассмотрения независимый пригожинский параметр, который реально расширяет размерность свойств нанообъектов.

Математика подобна снайперской винтовке, «мгновенно» поражающей цель на большом расстоянии («выстрел» Перельмана на тысячелетия). Однако этому мгновению предшествует длительное «вылизывание» каждой её детали (или, как сказал Эйнштейн, когда его спросили, как он сам дошёл до понимания теории относительности – я очень долго об этом думал). Только строгому математическому толкованию «1» коллективный французский «математик» Бурбаки посвятил целый том. А чтобы выйти на понимание многомерии в нашем 3-х мерном геометрическом пространстве мне пришлось, долгие годы, и проштудировать много томов по теоретико-групповому анализу, и провести многочисленные прецизионные эксперименты с помощью «ненужных» термоэлектрической «науке» методик, и научиться «видеть» (строить, изображать на бумаге) 3-х мерные сечения 4-х мерного пространства. Геометрические образы весьма полезны и 3-х мерные картинки в фазовом пространстве и в пространстве волновых векторов (Ферми-поверхность в зоне Бриллюэна) активно используются в физике твёрдого тела, но их размерность пришлось расширить.

Пришлось проламывать и стену непонимания, доказывая, «что так дальше жить нельзя». «Серость», ныне пролезшая в научные чинуши, предпочла, в своё время, не, как я предлагал ей на её «возражения» (от непонимания и неприятия того, что в букварях не описано), написать, как полагается учёным, просто опровержение моей статьи. «Серость» предпочла, уговорить, у меня за спиной, «научное» начальство отозвать мою статью, уже принятую в печать в нашем научном журнале, «как позорящую лицо лаборатории». Основной карьерный принцип «серости» – уничтожение конкурентов. И не случайно, а закономерно (более жёсткая зависимость, чем в законе Паркинсона) вознесение её на самые высокие посты в период застоя науки и девальвации истинно научных ценностей. Конечно, это существенно затормозило данное направление исследований у нас в России, которое я продолжал без всякой поддержки лаборатории и института. Поздравления с «великолепной работой» я получил только после её публикации много лет спустя за рубежом и получил только из-за рубежа. Но выходы за рамки ряда стандартных представлений, разрабатываемые в этой «многострадальной» работе, оказались очень кстати, как для понимания работ Ильи Пригожина, так и для определения причины «аномальности» наноявлений.

Для описания физических процессов и явлений необходимым условием является, естественно, учет всех существенных факторов, влияющих на них. Но простого учета разных факторов недостаточно для построения правильной теории. В физике есть такое понятие: нормальные (независимые) координаты, которое эквивалентно математическому понятию в теории множеств - ортогональный репер. Эти понятия введены для того, чтобы при математическом описании отсечь те кажущиеся закономерности (влияния), которые уже были прямо, либо косвенно учтены ранее. Т.е. начальная стадия моделирования сводится к определению минимального набора существенных факторов, достаточного для полного описания данного процесса или явления. Наглядный, и в прямом, и в переносном смысле, пример - это три независимые координаты для описания объемной фигуры. Двух координат достаточно для описания лишь фигур на плоскости и недостаточно для описания объема. Также как использование трех координат на плоскости, ничего нового не добавит для описания плоских фигур, но никак не поможет, а запутает (если специально не оговорить дополнительный параметр для третьей координаты) в описании объемной фигуры.

Таким образом, требование использовать именно минимальный набор координат (факторов) сводится к требованию использовать лишь независимые координаты. Несоблюдение этого требования (дублирование в расчётах того, что уже учтено, но исторически имеет другое название) и привело к ошибке в расчете барьера Шоттки и к погрешности в расчёте термоэлектрической эффективности Иоффе. В геометрическом пространстве это требование очевидно (опять же в прямом и переносном смысле). Хотя и в нашем трехмерном пространстве есть явления, долгое время воспринимавшиеся как «катастрофа» кристаллофизики. Когда были обнаружены объекты – несоразмерные кристаллы и фуллерены, кристаллическая структура которых не описывалась трехмерными (фёдоровскими) группами симметрии – то не сразу нашли объяснение, хотя симметрийный формализм (суперсимметрия) для этих объектов был давно развит в абстрактной многомерной математике и он давно использовался, скажем, в той же теории элементарных частиц. Исследования «эталонного» одномерно-несоразмерного кристалла ВСМ (S.V. Ordin, W.N. Wang, “Giant spatial dispersion in the region of plasmon-phonon interaction in one-dimensional- incommensurate crystal the higher silicide of manganese (HSM)”, in Book: Optical Lattices: Structures, Atoms and Solitons) показали, что для корректного описания подобных кристаллических структур и их свойств необходимы дополнительные измерения (прямое следствие суперсимметрии), в частности, для ВСМ – четвёртое геометрическое. Пользуясь случаем, приношу огромную благодарность профессору Вангу Нанг Вангу за помощь в этой работе.

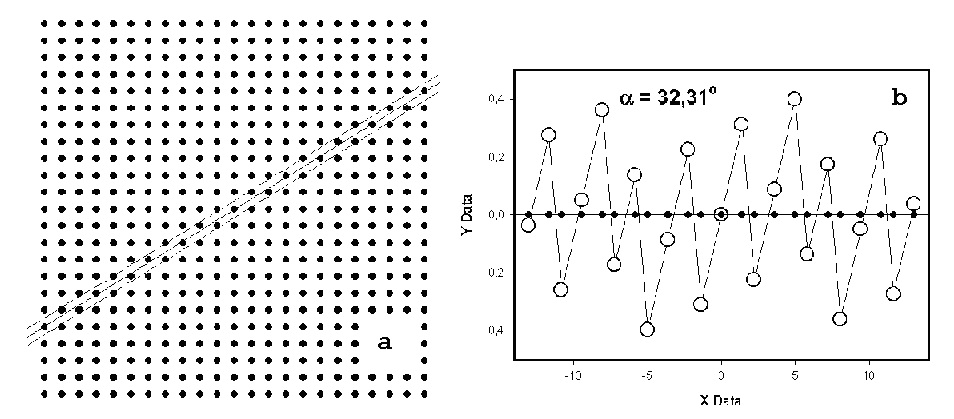
Профессор Ванг в семейном кругу на это Рождество.

В принципе, в этом расширении размерности нет ничего необычного и никакой мистики. В физике явлений давно используют матрицы и тензоры четвёртого и более высокого ранга и многомерные фазовые пространства. Но здесь требуется четвёртое геометрическое измерение, как для описания самой кристаллической структуры, так и возбуждений (волн) в ней. Но суть проста: вдоль некоторых направлений (в ВСМ вдоль одного) одной координаты недостаточно, как для описания всех процессов формирования кристаллической решётки, так и всех её свойств. Вдоль этого направления (совпадающего в ВСМ с главной осью симметрии С) существуют параллельно два независимых взаимодействия между атомами, приводящие к формированию двух независимых (слабосвязанных) вложенных друг в друга кристаллических подрешёток. Но независимые параметры – это ортогональные в математическом смысле параметры – и суммарному полному набору возможных вариантов двух параметров нужно сопоставлять плоскость, а не линию. Это можно наглядно и просто изобразить, как показано на рис. 1, в виде плоской решётки, тогда как её сечение линией может дать случайный и выглядящий хаотическим частный набор параметров.

Рис. 1. a - Элементарная решетка с эквивалентными параметрами трансляции. b - Отклонения ближайших точек (кружки) от плоскости сечения под рациональным углом через первоначально выбранную точку и их проекции на плоскость сечения (точки). При иррациональном угле – полное отсутствие трансляционной инвариантности – период повторения бесконечен, как для смещений, так и для проекций.

Рис.1 демонстрирует практически полное отсутствие трансляционной инвариантности в плоскости сечения регулярной решётки при не кратном угле сечения. Период повторения «скачет» при сколь угодно малом изменении одного из исходных параметров трансляции, что и привело к многочисленным результатам рентгеноструктурных исследований, каждое из которых «давало» ранее свою кристаллическую структуру ВСМ. Т.к. по первоначальному образованию я математик, то я не мог не заметить повторяющиеся вдоль оси С во всех известных структурах ВСМ цифры: 4 для атомов Mn и 2 -для атомов Si, но с разными периодами трансляции вдоль С. Это и позволило мне построить модель вложенных подрешёток, несоразмерных вдоль оси С, которая описала, как все наблюдаемые соразмерные структуры, в виде эффекта нониуса при условии термодинамической устойчивости структуры, так и наблюдаемые колебания соотношения атомов Mn и Si как концентрационные солитоны.

Так любое сечение плоскостью проходящей через ось несоразмерности 3-х мерной картины кристаллической решётки ВСМ даст хаотическое (беспорядочное расположение атомов вдоль оси С, а сечение плоскостью 4-х мерной картины даст регулярное расположение атомов одной из подрешёток. Можно было бы, казалось, просто рассматривать отдельно две 3-х мерные решётки. Но при решении общей задачи отклика кристалла на воздействие, да ещё при учёте, что хоть и слабое, но взаимодействие между подрешётками существует, суммарный отклик кристалла общий, и честно его можно рассчитать, лишь учтя все четыре измерения. Да и совершенный кристалл ВСМ вырастить до понимания 4-х мерности его решётки не удавалось, а после, с учетом твердофазного перехода через несоразмерную фазу – удалось. Также, как удалось описать большую совокупность свойств этого кристалла, ставшего модельным для несоразмерности.

Элементарный, но общий вывод: в «хаосе» можно найти закономерность, если учесть дополнительную (не учитываемую ранее), но существенную для рассматриваемого процесса независимую (ортогональную ранее введенным) координату. Данный подход позволил не только строго математически описать с помощью уравнения синус-Гордона кристаллические волны в несоразмерных кристаллах (концентрационные солитоны), и получить диэлектрическую проницаемость (в простейшем случае 4-х мерную) для фотонных кристаллов, но и предположить, что наблюдаемый нами хаос не так уж хаотичен, если представить его не как плоскую картину, а как объёмную с дополнительной координатой.

Часть 3. Энтропия, как мера хаоса.

В предыдущей части показано, что наличие неучтенного, но существенного параметра может привести к восприятию общей картины как полнейшего хаоса. Но и у хаоса, если система содержит очень большое число частиц, имеются четко определяемые интегральные и дифференциальные параметры. Макроскопические термостатика и термодинамика собственно и построены на базе таких статических и динамических параметров. Ниже будет показано, что при построении макроскопической термодинамики, учитывая только хаотическое (броуновское) движения частиц, упущено то, что собственно определяет локальные эффекты, которые возникают на микро/нано масштабе. Т.е. при макроскопическом рассмотрении отбрасывается независимый параметр, а все его значения как бы спроецированы на плоскость, построенную на макроскопических параметрах. При этом описываемые (разрешённые) макроскопической термодинамикой эффекты есть результат среднестатистический по всем значениям неучтенного параметра, а результаты расчетов при фиксированном значении неучтенного параметра (в сечении объемной картины плоскостью) хаотической термодинамикой запрещены. При этом, так как динамика хаоса описывалась лишь коэффициентами трения в линейных уравнениях связи сил и потоков, оказалось, что из термодинамического рассмотрения изначально выброшены нелинейные процессы, определяющие эффекты на микро/нано уровне.

Фундаментальным понятием для макроскопической (хаотической) термодинамики является энтропия. Энтропия σ характеризует наиболее вероятное состояние макросистемы, т.е. состояние, имеющее максимальное число g – число допустимых (микро) состояний частиц, составляющих эту систему или, как говорят иначе – степень вырождения системы. Но степень, и в прямом, и в переносном смысле – это логарифм. Логарифм σ = ln(g) удобнее использовать при количественных расчетах с большими числами и, как будет показано ниже, именно он связан с нашими макроскопическим ощущениям Природы – температурой. Энтропия σ позволяет с помощью комбинаторики количественно оценить энергию хаотического состояния U. Больцман качественно уловил связь энтропии (её производной по энергии состояния) с абсолютной температурой τ: 1/τ = dσ/dU, а благодаря вычислению Планком постоянной Больцмана k_Б, энтропия и количественно связывается с температурной шкалой Кельвина T: τ = k_Б T. Так как энтропия (степень) величина безразмерная, то абсолютная температура есть просто средняя энергия, приходящаяся на одну учитываемую в системе частицу при данной температуре.

Само понятие температура есть, по определению, величина, характеризующая тепловое равновесие между макросистемами с равными температурами. Аналогично и энтропия – макроскопическая характеристика равновесного состояния, которое находится из предположения, что число допустимых (микро) состояний g, как функция числа частиц N и суммарной энергии U имеет резкий максимум в точке равновесия. Поэтому, строго говоря, за рамками определения энтропии оказываются не только характеристики микрообъектов, содержащих ограниченное число частиц, но и макрообъекты, находящиеся в термодинамически неравновесном состоянии (практически бесконечно долго, как например, алмаз). Конечно, это не могли не заметить ранее. И были проведены многочисленные термодинамические расчеты так называемых, метастабильных состояний, но все эти расчеты, до Ильи Пригожина, велись из предпосылок вычисления малых поправок к равновесному состоянию (пример, разложение по параметру малости Ландау при фазовых переходах). И проверка результатов таких расчетов велась опять же с помощью макроскопических законов сохранения (масло масляное). Фактически резко переменную (на наномасштабе) функцию описывали линейной аппроксимацией макроскопической зависимости при приближении к нулю. Хотя иногда и делали «открытия» в расчетах о гигантских отклонениях от линейной функции, но, при этом, скромно умалчивали, что с помощью параметров малости можно считать лишь малые (а не гигантские, катастрофические) поправки. А умалчивали, во многом по тому, что боялись даже в мыслях предположить, что использованный при расчетах базовый закон не работает.

В этом плане, за рамками макроскопической термостатики и её современного продолжения – линейной неравновесной термодинамики оказываются некоторые макроскопические, но меньшего масштаба, чем рассматриваемые диффузные (ламинарные) потоки, эффекты, такие, как кавитация и флаттер. Требуемые для этих явлений «локальные» энергии на порядки превосходят те, что следуют из дифференциальных характеристик хаотических потоков. А сама возможность вырвать куски металла из гребного винта или возможность обрушить летящий самолет, в рамках используемых теорий на базе усредненного хаоса, является «малой» поправкой к «проверенной» теории. Но это в корне не верно (почему, собственно, эти науки и фрагментированы от термодинамики – иначе бы они попали в разряд запрещенных). Малая поправка, по определению, должна быть мала. Малая поправка может играть роль спускового крючка, если не учтены некоторые существенные факторы: если она является поправкой в точке перевала. Но само наличие этой точки перевала требует учета дополнительного параметра, не учитываемого ранее, т.е. расширения размерности анализируемой картины. В термодинамике, макроскопической, не учтен масштаб, который проявился при достижении технологией наноуровня. Если в макрокристалле алмаза можно пользоваться макроскопическими термодинамическими характеристиками как внутри самого кристалла, так и при его тепловом контакте с другими макрообъектами, подразумевая, как данность, что вплоть до температуры разрушения алмазных межатомных орбиталей (в графите они другие) он неизменен, то нанокристаллы «алмазов», в случае хаотического распределения «орбиталей» между ними, сами могут рассматриваться как «микрочастицы» макросистемы (что, во многом, можно отнести к нанотранзисторам в интеловских процессорах, что, и определяет их низкую производительность). Но внутри наноалмазов применять макроскопические термодинамические характеристики даже в нулевом приближении, не корректно, т.к. по определению некорректна линейная аппроксимация в ноль макроскопических характеристик, справедливых лишь для большого числа частиц. А то, что таких «алмазиков» вокруг нас как грязи (в прямом и переносном смысле), стало понятно теперь даже тем, кто закончил всего лишь Академию КГБ.

Часть 4. Порядок в хаосе.

Попытки осмысления (описания) хаоса предпринимались давно (см. например, книгу Дж. Займана «Теория хаоса») И то, что порядок возникаете и в хаосе на макромасштабе, я постараюсь показать наглядно ниже. Но если для хаоса введена описанная выше нормальная координата, которую можно измерять: мера хаоса – энтропия, то мера порядка в хаосе на микро/нано уровне пока даже не предусмотрена, а тем более не определена количественно. Это и приводит к макроскопическому подходу, как при постановке экспериментов на наномасштабе, так и их обсчитыванию, а как следствие, к чисто эмпирическому развитию нанотехнологии.

На макроскопическом уровне простейшее «упорядочение» хаоса фактически описывает неравновесная термодинамика. Это перекрестные эффекты между тепловой силой (градиентом температуры) и другими обобщёнными термодинамическими силами (электрическими, гравитационными, концентрационными и прочими). Но за рамками данного подхода возникает упорядочение на разных масштабах. На космических масштабах – формирование планетарных систем и галактик. На земных масштабах – бури, цунами, а более локально – смерчи, тайфуны. На масштабах больше и порядка микрометров в кристаллах – электроны и дырки с эффективной массой, экситоны, концентрационные солитоны, плазменные волны и прочие коллективные эффекты макроскопического ЧИСЛА частиц. Многое из этого описано, например, в книге Власова «Теория многих частиц» ещё до ВОВ на базе тогда популярного интегро-дифференциального исчисления. Многое в учебниках физики твёрдого тела. Современные исследователи этих явлений во многом преуспели в описании макроскопических явлений (хотя смерч, поднимающий воду на 3 км, когда за счёт разряжения её можно поднять не более чем на 12 м и когда вращение должно разбрасывать воду и воздух, а не сжимать, по-моему, пока не описан). Многое сделано и в так называемых микроскопических теориях типа физики твёрдого тела. Современные исследования макроскопических «отклонений» от линейной неравновесной термодинамики выделились в отдельные «науки», которые, естественно, так как это видно невооружённым взглядом, рассматривают эти процессы не как малые поправки к линейным потокам. И исследователи не очень обеспокоены связью своих наук с термодинамикой. Хотя, на мой взгляд - зря. Те же космологи не высасывали бы свои теории из пальца.

Но в данной статье о наноявлениях, естественно, я остановлюсь преимущественно на особенности данного масштаба.

Теоретический запрет на нарушение хаоса на микро/нано уровне, в какой-то мере, связан с канонизацией распределения Больцмана для классических частиц и распределений Ферми-Дирака и Бозе-Эйнштейна для квантовых частиц, используемых для расчёта состояния макроскопической электронной системы. Но, в принципе, под этот запрет попадают и уже эмпирически созданные и работающие нанотранзисторы, и уже выращенные нанотрубки, т.к. не являются термодинамически равновесными, как, например, кристалл и свойства их противоречат макроскопическим формулам. Хотя их (запрещенные) свойства пытаются рассчитывать по формулам, полученным опять же в рамках макроскопических представлений (для бесконечного числа частиц). Таков парадокс современной нанофизики. Теоретики своими глазами (ощущениями) не могут увидеть «смерчи» на микро/нано уровне, а опираются на интерпретации экспериментов в рамках разработанных макроскопических представлениях, которые, естественно, на выходе дают макроскопические параметры, а характеристики «смерчей» на наноуровне и не предусмотрены. И, тем самым, после этого масла масляного, тупо лепят горбатого об общей справедливости макроскопической статистики и линейной неравновесной термодинамики, хотя их предсказания-расчеты давно уже не работают и используются исключительно для защиты диссертаций. Но на масштабе меньше длины свободного пробега, как было показано ранее, возникают не малые поправки к линейному (ламинарному) потоку. Но среднестатистическое распределение электронов над совокупностью потенциальных барьеров не есть мгновенное их распределение над каждым индивидуальным барьером наномасштаба и постулат – усреднение по пространству эквивалентно усреднению по времени – на наномасштабе не работает.

А что работает?

Работает честный расчет индивидуальных параметров электронов в электрическом поле вблизи отдельного определённого барьера.

Так как по «духу» я математик то я не мог пройти мимо ошибки в общем решении элементарной математической задачи ускорения свободного электрона физиками, упускающем особенность при малых скоростях. Честная формула

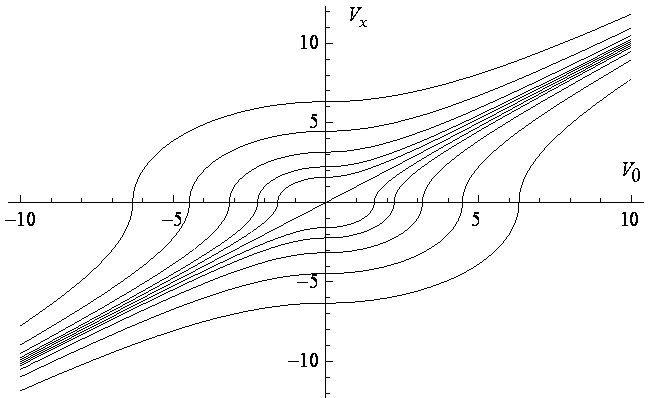
даёт неучтенную особенность, показанную на рис. 2

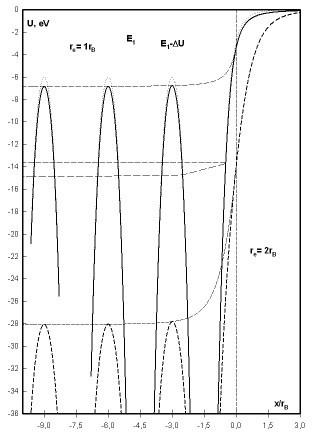
Рис. 2. Зависимость конечной скорости электронов V_x после прохождения расстояния от их начальной (тепловой) скорости V₀. Разность потенциалов eEx для смежных кривых отличается в 2 раза.

Эта элементарная математическая ошибка приводит к существенным ошибкам, как в некоторых моделях физики твёрдого тела, так и в моделях физики термоэмиссии.

Но и сам барьер, уже надо рассматривать не как прямоугольный «теоретический» кирпич (в физике атома на масштабах гораздо меньших атома), а как сумму (аддитивный вклад) атомных потенциалов конкретного числа атомов, дающих локальные энергетические нанозоны. В атомной физике давно уже поняли, что даже уровни электронов в отдельных атомах правильно не рассчитать, если не учесть истинную пространственную дисперсию потенциала атома на масштабе много меньше нано. А в твёрдом теле продолжают тупо использовать прямоугольники вместо представленного на рис. 3 распределения.

Как видно из рис. 3, и на границе группы атомов с вакуумом дисперсия потенциала сильно зависит от числа атомов (и ряда других параметров), и внутри группы атомов дисперсия потенциала никак не равна нулю, хотя выше максимумов потенциала электроны могут свободно двигаться.

Также надо учитывать как взаимное влияние потенциалов соседних барьеров, так и электронов, связанных с отдельными барьерами.

Но есть ещё НЕЧТО, что связано с локальной самоорганизацией тех же электронов, что и определяет локальное нарушение хаоса и, тем самым, требующее учёта локальной термодинамики. И это НЕЧТО имеет тенденцию к самосохранению, нарушающую макроскопическую статистику, что принципиально отличает его как от среднестатистических флуктуаций. Это НЕЧТО описывается статистикой с накоплением информации и связано, как позволили себе заявить нобелевские лауреаты Манфред Эйген и Рутхильд Винклер с зарождением самой жизни (М. Эйген, Р. Винклер. Игра жизни, Москва, Наука, 1979)

Это своего рода электронные солитоны, но которые имеют тенденцию к самосохранению иную, чем у обычных солитонов – опиисываемый уравнением синус-Гордона коллективный эффект при неограниченном числе частиц – волны на мелкой воде. Это и не квазичастица, которая, опять же – коллективный эффект всей совокупности электронов в кристалле. Это коллективный эффект за счёт потенциального минимума в энергии связи частиц на пропущенном наномасштабе. На этом масштабе, строго говоря, классических измерений сил притяжения и отталкивания не проводили, а логический вывод, как для атомных и ядерных сил из стабильности атомов и ядер, не делали. Даже для молекул старались всё свести к межатомному взаимодействию, которое талантливые химики и технологи «нарушали» создавая уникальные материалы. Делали не строго по «науке», как и отмеченный ранее талантливый электронщик, но получали решение задачи, умышленно вводя погрешность в формулы, т.к. не относились к ним как к ЗАКОНУ. Аналогично строго установленным химическим формулам наночастицы (фулерены, нанотрубки) демонстрируют энергетическую стабильность, но на данном масштабе даже при нарушении определённого числа межатомных связей. Возможно, это НЕЧТО проявляется и в росте кристаллов, т.к. их рост начинается с формирования нанозародышей кристаллизации. Возможно, это НЕЧТО и почувствовал Илья Пригожин в первую очередь как химик, не полностью удовлетворённый используемым физическим описанием, за что «писатели» поставленного им под сомнение «описания», физики, его, естественно, и невзлюбили.

Это НЕЧТО и приводит как к неоднородности распределения частиц в пространстве, так и к особенности в энергетическом распределении частиц, принципиально отличной от монотонных «хвостов» макроскопических распределений Больцмана, Ферми-Планка и Бозе-Эйнштейна. В этом их принципиальное отличие от рассмотрения просто большого числа молекул со средней температурой – из данного в предыдущей главе достаточно подробного описания макроскопического параметра – температура – видно, что внутри такой отдельной «молекулы» определять температуру некорректно. Корректно, видимо, применить статистику с накоплением информации из отмеченной выше книги М. Эйгена и Р. Винклера.

На атомном уровне это самосохраняющееся НЕЧТО проявилось в возникновении обнаруженных Александром Козеевым самоподдерживаемых фулереновых циклов и по-видимому «помогает» выращивать нанотрубки и нанотранзисторы.

Для этого НЕЧТО можно ввести независимую локальную термодинамическую силу, учёт которой позволит снять противоречия в расчётах и сделает их рабочим инструментом как при создании нанообъектов, так и при описании их свойств (перекрёстных с этим НЕЧТО эффектов). Учёт этой локальной термодинамической силы и снимает запрет на существование «аномальных» термоэлектрических эффектов (Ordin S.V., Zjuzin A. Yu., Ivanov Yu.and Yamaguchi S., "Nano-structured materials for thermoelectric devices", NATO Workshop "Advanced Materials and Technologies for Micro/Nano-Devices, Sensors and Actuators" June 29 - July 2, 2009, St Petersburg, Russia; S.V. Ordin, W.N. Wang, "Thermoelectric Effects on Micro and Nano Level.", J. Advances in Energy Research, Volume 9, 2011, 30 pp.), на базе которых уже созданы работающие устройства.

Локальная сохраняемость звучит коряво и длинно. Я бы просто назвал эту независимую координату «выживаемости» кластеров частиц в наномире – степень сцепления (в коментах мне подсказали ещё одно название – «брачность» частиц, но тут, на наноуровне возможны многобрачные семьи). А нанодом, в котором «выживаемость» максимальна, и есть термодинамически устойчивый нанообъект с учётом локальной термодинамики «сцепившихся» на наномасштабе частиц (термодинамически устойчивый, но не термодинамически равновесный). На мой взгляд, термины «выживаемость» и «сцепление» ничем не хуже «шарма» у физиков элементарных частиц, но ближе к ощущению людей (что за «шарм», «вкус» и «цвет» у абстрактных теоретиков можно только предполагать). И это, возможно, не случайно. И принципы квантовой механики базируются на принципах психологического восприятия человеком этого Мира. И «выживаемость» самой жизни заложена на наноуровне. Правда, выживаемость самих людей определяется другим «масштабом». Но это уже относится к теории различимых частиц.

Заключение.

Так «абстрактные» рассуждения о единстве реальной Природы позволяют выявить ошибки и упущения в фрагментированной физике, фрагментированной как внутри её самой, так и от таких смежных наук, как химия и математика. Осталось дело за малым: переписать ещё некоторые формулы с учётом данной нормальной координаты наномасштаба – новой ортогональной координаты – и научиться её измерять. Но это конечно не так просто. Силы на наномасштабе переплетены, и вместо привычных линейных матричных соотношений надо, на самом деле, строить новые честные формулы функции многих переменных. И при этом постоянно следить за собой, чтобы не свалиться в привычную, «любимую» за свою простоту, линеаризацию, которая не даёт на наномасштабе даже нулевого приближения к Реальности.

Но представленные в этой статье «варварские» рассуждения конечно не годятся для «окультуренных» «Успехов Физических Наук», хотя за этими рассуждениями сотни страниц описания исправлений канонизированных моделей, сотни файлов с экспериментальными данными и сотни файлов с численным моделированием. Хотя эти работы, как отмечал выше, за рубежом уже очень востребованы. Ну что ж, пусть перепечатывают мои статьи из зарубежных журналов.

В «окультуренной» же России, после моего Открытого Письма «Табу на прогресс науки», хоть и убрали тоже в явном виде из правил запрет на переписывание феноменологии в правилах приёма статей, но подспудно это Табу сохраняется. Сохраняется «окультуренными», а на самом деле невежественными чинушами от российской науки. И пока поиск Истины не станет определяющим в российской науке, этой «науке» будет грош цена.